Stanford CS234 Lecture2

Stanford CS234: Reinforcement Learning | Winter 2019 | Lecture 2

Given the model of the world

Markov Property → stochastic process evolving over time(whether or not I investi stocks, stock market changes)

Markov Chain

• sequence of random states with Markov property
• no rewards, no actions

Let $S$ be set of states ($s\in S$) and $P$ a transition model that specifies $P(s_{t+1}=s^{\prime }|s_t=s)$

for finite number($N$) of states, we get transition matrix $P$

example discussed last section(we abort discussion of rewards and actions for easy understanding)

at state $s_1$ we have 0.4 chance of transfering to $s_2$ ($P(s_1|s_2)$) and 0.6 probability of staying $s_1$ ($P(s_1|s_1)$). Such probability matrix is expressed as $P$ above.

Let’s say we start at $s_1$, we can calculate agent’s probablility of next state by calculating dot product of $[1,0,0,0,0,0,0]$ and $P$ above. As result we get $[0.6,0.4,0,0,0,0,0{]}^T$

---

Markov Reward Process(MRP)

• Markov Chain + rewards
• no actions

for finite number($N$) of states,

$S$ : set of states ($s\in S$)

$P$ : transition model that specifies $P(s_{t+1}=s^{\prime }|s_t=s)$

$R$ : reward function $R(s_t=s)=E[r_t|s_t=s]$

Horizon

• number of time steps in each episode
• can be either finite or infinite

Return($G_t$)

• Discounted sum of rewards from time step t to horizon

$$G_t=r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+{\gamma }^3{r}_{t+3}+...$$

State Value Function(V(s))

• ‘Expected’ return from starting in state $s$ → average of all returns at state $s$
• $V$ is defined for each state $s$ thus may be displayed in array format.

$$V(s_t=s)=E[G_t|s_t=s]=E_{\pi }[r_t+\gamma r_{t+1}+{\gamma }^2{r}_{t+2}+{\gamma }^3{r}_{t+3}+...|s_t=s]$$

if the process is deterministic Return = State Value → since there would be single identical route .

Example

return value for sample episode, where $\gamma =0.5$

episode $s_4$→$s_5$→$s_6$→$s_7$ , $return$ : $0+0.50+0.5^20+0.5^3*10=1.25$

Computing the Value of Markov Reward Process

• can estimate by mathematical simulation
• MRP value function satisfies

$$V(s)=R(s)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s)V(s^{\prime })$$

• Proof

Matrix form of Bellman Equation for MRP

• analytic method of calculation

for finite MRP, we know $R(s)$ and $P(s|s)$, we express $V(s)$ in matrix eqn

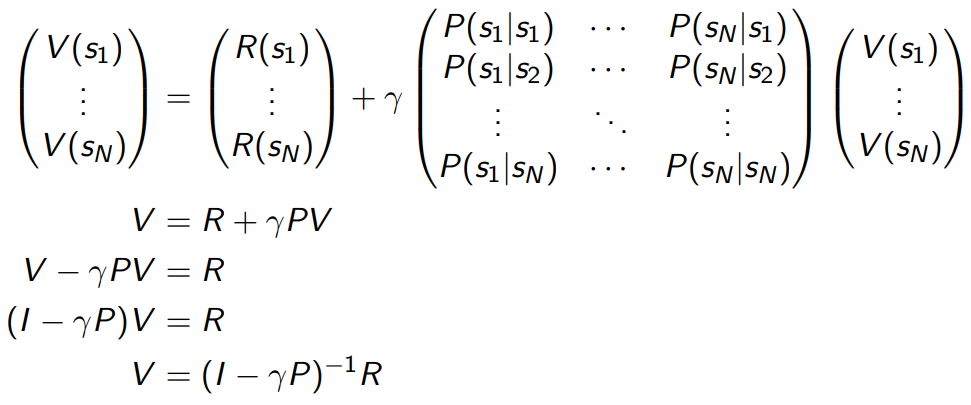
Iterative Algorithm for Computing Value of a MRP

Dynamic Programming

• Initialize $V_0(s)=0$ for all s

for k = 1 until convergence

for all $s$ in $S$

$V_k(s)=R(s)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s)V_{k-1}(s^{\prime })$

** computational complexity is simpler compared to analytical method

---

Markov Decision Process(MDP)

• Markov Reward Process + actions

for finite number($N$) of states,

$S$ : set of states ($s\in S$)

$A$ : set of actions($a\in A$)

$P$ : transition model for each action $P(s_{t+1}=s^{\prime }|s_t=s,a_t=a)$

$R$ : reward function $R(s_t=s,a_t=a)=E[r_t|s_t=s,a_t=a]$

MDP is a tuple: ($S,A,P,R,\gamma$)

Example

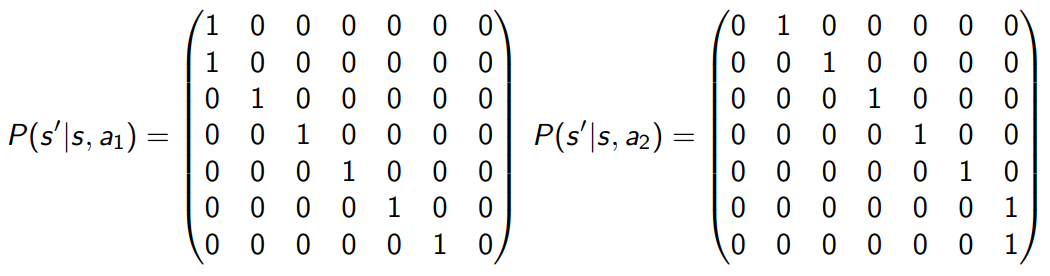
action $a_1$ : move left, action $a_2$ : move left

MDP policies can be either *deterministic(I always do this in this state) or stochastic(there exists set of possible actions for this state)*

Markov Decision Process

• MDP + $\pi (a|s)$ ⇒ MRP ($S,R^{\pi },P^{\pi },\gamma$)

$$R^{\pi }(s)=\sum _{a\in A}\pi (a|s)R(s|a)$$

$$P^{\pi }(s^{\prime }|s)=\sum _{a\in A}\pi (a|s)P(s^{\prime }|s,a)$$

MDP Policy Evaluation - Iterative Algorithm

• Initialize $V_0(s)=0$ for all s

for k = 1 until convergence

for all $s$ in $S$

$V_k^{\pi }(s)=r(s,\pi (s))+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,\pi (s))V_{k-1}^{\pi }(s^{\prime })$

this is a Bellman backup for particular policy

Example

!

only two actions $a_1,a_2$ and let’s say $\pi (s)=a_1,\gamma =0$

compute iterations!

$V_k^{\pi }(s)=r(s,\pi (s))+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,\pi (s))V_{k-1}^{\pi }(s^{\prime })$

since $\gamma =0$, $V(s_4)$ would be zero with only its immediate reward

Practice

• Dynamics : $p(s_6|s_6,a_1)=0.5,p(s_7|s_6,a_1)=0.5$
• Let $\pi (s)=a_1,V_k^{\pi }=[1,0,0,0,0,0,10]$ and $k=1,\gamma =0.5$

Find $V_1^{\pi }(s_6)$.

— — — — — — — — — — — — — — — — — — — — — — — — — — —

$$
V^\pi_2(s_6)=0 + 0.5(0.50+0.510)=2.5
$$

MDP Control

• compute optimal policy

$${\pi }^{\ast }(s)=\arg \underset{\pi }{max}{V}^{\pi }(s)$$

• there exists a unique optimal value function
• Optimal policy for an infinite horizon MDP→ Stationary (in same state, time stamp doesn’t matter)
• → not necessarily unique since there may exist other state-action with same optimal value
• → Deterministic

* optimal policy is not unique whereas an optimal value function is unique

Question

---

MDP Policy Iteration(PI)

for infinite horizon,

State-Action Value $Q$

$$Q^{\pi }(s,a)=R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{\pi }(s^{\prime })$$

immediate reward + expected reward starting from next state, following $\pi$

Policy Improvement(steps)

1. compute all $Q$ values for all $S$ ans $A$

$$Q^{{\pi }_i}(s,a)=R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,a)V^{{\pi }_i}(s^{\prime })$$

1. compute new ${\pi }_{i+1}$ for all $S$ that maximizes $Q^{{\pi }_i}$

$${\pi }_{i+1}(s)=arg\underset{a}{max}{Q}^{{\pi }_i}(s,a)$$

    $\pi_{i+1}$ is either $\pi_i$ or a different $a$ that maximized $Q$ value thus

$$\underset{a}{max}{Q}^{{\pi }_i}(s,a)\ge Q^{{\pi }_i}(s,{\pi }_i(s))=R(s,{\pi }_i(s))+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s,{\pi }_i(s))V^{{\pi }_i}(s^{\prime })=V^{{\pi }_i}(s)$$

“if we took a new policy for an action and then follow ${\pi }_i$ forever, we’re guaranteed to be at least as good as we were before in terms of value function.”

Monotonic Improvement in Policy Value

the new policy is greater than equal to the old policy for all states

Proposition : $V^{{\pi }_{i+1}}\ge V^{{\pi }_i}$ with strict inequality if ${\pi }_i$ is suboptimal, where ${\pi }_{i+1}$ is the new policy we get from policy improvement on ${\pi }_i$.

• Proof
• 

MDP Value Iteration (VI)

• Know optimal value and policy but only gets to act for $k$ time steps

Bellman Equation and Bellman Backup Operators

Bellman Equation → Value fucntion of a policy must satisfy

$$V^{\pi }(s)=R(s)+\gamma \sum _{s^{\prime }\in S}{P}^{\pi }(s^{\prime }|s)V(s^{\prime })$$

Bellman backup operator

• applied to a value function and return a new value function
• yields a value function over all states $s$

$$BV(s)=R(s,a)+\gamma \sum _{s^{\prime }\in S}P(s^{\prime }|s)V(s^{\prime })$$

Policy Iteration as Bellman Operations

• Bellman backup operator $B^{\pi }$ for particular policy

$$B^{\pi }V(s)=R^{\pi }(s,a)+\gamma \sum _{s^{\prime }\in S}{P}^{\pi }(s^{\prime }|s)V(s)$$

• repeatedly apply operator until $V$ stops changing for evaluation

$$V^{\pi }=B^{\pi }{B}^{\pi }...B^{\pi }V$$

Value Iteration(VI)

Contraction Operator

• Let $O$ be an operator and $|x|$ denote norm of $x$
• if $|OV-O{V}^{\prime }|\le |V-V^{\prime }|$, then $O$ is a contractiion operator
• → the distance between two vectors can shrink applying certain operator

Question : Will Value Iteration Converge?

A : Yes, because Bellman backup is a contraction operator

• Proof
• 

---

참고할 링크

[https://sumniya.tistory.com/5](