로봇의 위치와 바라보는 방향을 합쳐서 Pose라고 한다. Pose는 position과 orientation으로 구성되며 기준이 되는 reference frame을 필요로 한다. 가령 world frame(F{w})을 상에 아래와 같은 로봇이 위치한다면 이는 F{w}의 (0,0)을 기준으로 그 위치와 orientation을 설명할 수 있다.

실제 로봇의 경우 센서를 통해 감지되는 물체를 판단할 때 스스로를 새로운 frame(F{R})의 중심으로 해당 물체의 위치를 판단한다. 이 때 global frame 상에서의 물체의 위치는 robot frame에서의 좌표와는 다를 것이다.

2D 환경에서 고정된 global frame을 기준으로 새로운 frame이 발생할 때 이동한 frame 은 Translation과 Rotation 두 가지 행동으로 설명이 가능하며 이 두 가지를 합쳐 Transform이라 칭한다. 이동한 frame 상의 좌표는 간단한 행렬 연산으로 global frame 좌표로 변환할 수 있다. 기본적인 Translation과 Rotation의 경우 아래와 같다.

두 가지가 동시에 일어나는 Transform의 경우도 행렬 곱으로 연산이 가능하다.

위 방식으로 2D transformation은 전부 해석이 가능하다.
3D frame의 경우 축이 하나 추가된다. 3축 해석은오른손 법칙에 따른다.

3D 공간 상의 로봇의 좌표는 x,y,z 요소로 구성되며 로봇이 생성하는 frame도 3축의 frame이다. 각 축에 대한 회전은 robotics에서는 yaw(z), pitch(y), roll(x)로 구분한다.

한 축에 대해서만 회전이 존재하던 2D frame과 달리 3D frame에서는 세 축에 대한 회전이 가능하며 각 frame에 대해 다른 rotation matrix가 존재하고 세 matrix 연산을 통해 global rotation matrix를 찾을 수 있다.

결론적으로 필요한 것은 Rg이며 robot frame 상의 좌표를 global frame의 좌표로 변환하는 식은 아래와 같다.
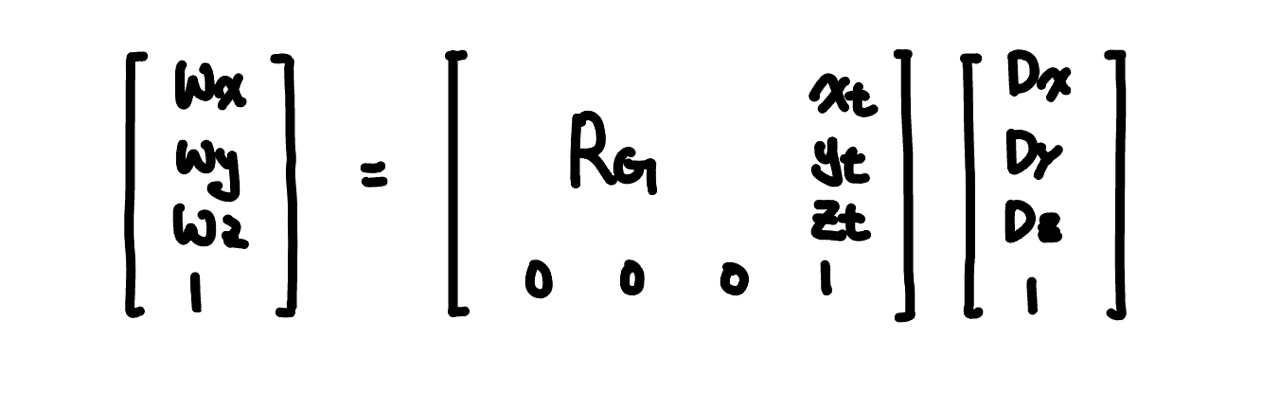
끝.
'ROBOTICS > Robot Localization' 카테고리의 다른 글
| 이론 : TF package의 이해 (0) | 2022.10.17 |
|---|---|
| 이론 : Orientation in 3D Space (0) | 2022.10.06 |
| Topic 정리 (0) | 2022.09.28 |



댓글